|
|
After experimentation has been completed, and a process or design has been
optimized, it is not uncommon for the experimentation team to consider the
problem to be solved. In many cases, the optimum solution does not stay optimum;
equipment changes as it ages, the composition of components change over time,
and many other factors make small changes that affect the response variable.
Evolutionary Operation (EVOP) is a method of addressing the constant small
changes in a process in attempt to maintain an optimum level. Experimentation is
carried out on a near continuous basis by introducing small changes to the
system.
One of the most popular methods of EVOP is sequential simplex optimization.
The simplex is a geometric figure with the number of vertexes equal to the
number of factors plus one. A simplex with one factor is a line, a simplex with
two factors is a triangle, etc. The simplex is a simplistic model of the
surface. a new simplex is formed by eliminating the vertex with the worst
response and replacing it by projecting it through the average coordinates of
the remaining vertexes. A new experiment is performed with the factor levels
determined by the coordinates of the new vertex, and the process is repeated
until an optimum response is found. Using the sequential simplex method
optimization has two advantages over using factorial designed experiments for
EVOP.
- The number of trials in the initial simplex is k+1 (k is the number
of experimental factors), while a factorial approach has at least 2k
and possibly 3k or 4k.
- Only one new trial is required to move to a new area in the space defined
by the factors; while a factorial design requires at least 2k-1
trials. An example of a sequential simplex optimization is shown in the
figure below.
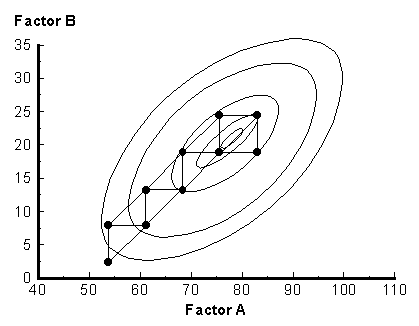
To compute the coordinates of the new vertex (R), refer to the following
table, where B is the vertex with the best response, N is the vertex with the
next best response, and W is the vertex with the worst response. This table
shows an example for a 3 factor optimization (k = 3). The logic is the
same for any number of factors.
|
A
|
B
|
C
|
Result
|
|
Next Best
|
20
|
20
|
20
|
425
|
|
Best
|
20
|
30
|
20
|
503
|
|
Other
|
30
|
20
|
20
|
378
|
|
Sum
|
70
|
70
|
60
|
|
|
Sum/k
|
23.3
|
23.3
|
20
|
|
|
Worst
|
20
|
20
|
15
|
215
|
|
Sum/k-W
|
3.3
|
3.3
|
5
|
|
|
R
|
26.7
|
26.7
|
25
|
|
|
(Sum/k-W)/2
|
1.7
|
1.7
|
2.5
|
|
|
Cw
|
21.7
|
21.7
|
17.5
|
|
|
Cr
|
25
|
25
|
22.5
|
|
|
E
|
30
|
30
|
30
|
|
The optimum point is never reached in the figure above because the size of
the individual simplex is too large. If the simplex size is too small, an
excessive number of steps is required to reach the optimum point. This problem
has been solved by using a variable size simplex. Instead of a simple reflection
(R), there are other options:
- double the length of the reflection (E),
- reduce the length of the expansion by 50% (Cr),
- produce the reflection in the opposite direction (W), and
- produce the reflection in the opposite direction but at 50% of the normal
length (Cw).
The additional rules for determining the location of the new vertex are:
- If the response for the new vertex (R) is better than the response for the
next best vertex (N), but worse than the response of the best (B) vertex,
then use R as the new vertex.
- If the response for the new vertex (R) is better than the response of the
best vertex (B), then compute E = P + 2(P-W).
- If the response of E is better than the response of B, use E as the new
vertex; if not, use R as the new vertex.
- If the response for the new vertex (R) is worse than the response of the
next best vertex (N) but better than the response of the worst vertex (W),
then compute Cr = P + 0.5(P-W) as the new vertex.
- If the response for the new vertex (R) is worse than the response of the
worst vertex (W), then compute Cw = P - 0.5(P-W) as the new vertex.
Example
Consider the parameter Y determined from the function Starting with the
vertices
Y = 40A + 35B - 15A2 - 15B2 + 25AB
Solution
Starting with the vertices
| Vertex |
A |
B |
Response |
| 1 |
100 |
100 |
-42,500 |
| 2 |
100 |
120 |
-57,800 |
| 3 |
120 |
120 |
-63,000 |
The response Y is maximized using a variable-step sequential simplex as shown
below.
|
Start
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
100 |
100 |
-42500 |
B |
|
| Next
Best (N) |
100 |
120 |
-57800 |
N |
|
| Sum |
200 |
220 |
|
|
|
| P bar |
100 |
110 |
|
|
|
| Worst (W) |
120 |
120 |
-63000 |
W |
|
| P bar - W |
-20 |
-10 |
|
|
|
| Next Vertex (R) |
80 |
100 |
-39300 |
R |
Compute
E |
| E
= |
60 |
90 |
-34950 |
|
Use
E |
|
|
|
|
|
|
|
Step 2
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
60 |
90 |
-34950 |
B |
|
| Next
Best (N) |
100 |
100 |
-42500 |
N |
|
| Sum |
160 |
190 |
|
|
|
| P bar |
80 |
95 |
|
|
|
| Worst (W) |
100 |
120 |
-57800 |
W |
|
| P bar - W |
-20 |
-25 |
|
|
|
| Next Vertex (R) |
60 |
70 |
-17650 |
R |
Compute
E |
| E
= |
40 |
45 |
-6200 |
|
Use
E |
|
|
|
|
|
|
|
Step 3
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
40 |
45 |
-6200 |
B |
|
| Next
Best (N) |
60 |
90 |
-34950 |
N |
|
| Sum |
100 |
135 |
|
|
|
| P bar |
50 |
67.5 |
|
|
|
| Worst (W) |
100 |
100 |
-42500 |
W |
|
| P bar - W |
-50 |
-32.5 |
|
|
|
| Next
Vertex (R) |
0 |
35 |
-17150 |
R |
Use
R |
|
|
|
|
|
|
|
Step 4
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
40 |
45 |
-6200 |
B |
|
| Next
Best (N) |
0 |
35 |
-17150 |
N |
|
| Sum |
40 |
80 |
|
|
|
| P bar |
20 |
40 |
|
|
|
| Worst (W) |
60 |
90 |
-34950 |
W |
|
| P bar - W |
-40 |
-50 |
|
|
|
| Next Vertex (R) |
-20 |
-10 |
-3650 |
R |
Compute
E |
| E
= |
-60 |
-60 |
-22500 |
|
Use
R |
|
|
|
|
|
|
|
Step 5
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
-20 |
-10 |
-3650 |
B |
|
| Next
Best (N) |
40 |
45 |
-6200 |
N |
|
| Sum |
20 |
35 |
|
|
|
| P bar |
10 |
17.5 |
|
|
|
| Worst (W) |
0 |
35 |
-17150 |
W |
|
| P bar - W |
10 |
-17.5 |
|
|
|
| Next Vertex (R) |
20 |
0 |
-5200 |
R |
Use
R |
|
|
|
|
|
|
|
Step 6
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
-20 |
-10 |
-3650 |
B |
|
| Next
Best (N) |
20 |
0 |
-5200 |
N |
|
| Sum |
0 |
-10 |
|
|
|
| P bar |
0 |
-5 |
|
|
|
| Worst (W) |
40 |
45 |
-6200 |
W |
|
| P bar - W |
-40 |
-50 |
|
|
|
| Next Vertex (R) |
-40 |
-55 |
-17900 |
R |
Compute
Cw |
| Cw
= |
20 |
20 |
-500 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 7
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
20 |
20 |
-500 |
B |
|
| Next
Best (N) |
-20 |
-10 |
-3650 |
N |
|
| Sum |
0 |
10 |
|
|
|
| P bar |
0 |
5 |
|
|
|
| Worst (W) |
20 |
0 |
-5200 |
W |
|
| P bar - W |
-20 |
5 |
|
|
|
| Next Vertex (R) |
-20 |
10 |
-12950 |
R |
Compute
Cw |
| Cw
= |
10 |
2.5 |
-481 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 8
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
10 |
2.5 |
-481 |
B |
|
| Next
Best (N) |
20 |
20 |
-500 |
N |
|
| Sum |
30 |
22.5 |
|
|
|
| P bar |
15 |
11.25 |
|
|
|
| Worst (W) |
-20 |
-10 |
-3650 |
W |
|
| P bar - W |
35 |
21.25 |
|
|
|
| Next Vertex (R) |
50 |
32.5 |
-9581 |
R |
Compute
Cw |
| Cw
= |
-2.5 |
0.625 |
-217 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 9
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
-2.5 |
0.625 |
-217 |
B |
|
| Next
Best (N) |
10 |
2.5 |
-481 |
N |
|
| Sum |
7.5 |
3.125 |
|
|
|
| P bar |
3.75 |
1.5625 |
|
|
|
| Worst (W) |
20 |
20 |
-500 |
W |
|
| P bar - W |
-16.25 |
-18.4375 |
|
|
|
| Next Vertex (R) |
-12.5 |
-16.875 |
-2432 |
R |
Compute
Cw |
| Cw
= |
11.875 |
10.78125 |
194 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 10
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
11.875 |
10.78125 |
194 |
B |
|
| Next
Best (N) |
-2.5 |
0.625 |
-217 |
N |
|
| Sum |
9.375 |
11.40625 |
|
|
|
| P bar |
4.6875 |
5.703125 |
|
|
|
| Worst (W) |
10 |
2.5 |
-481 |
W |
|
| P bar - W |
-5.3125 |
3.203125 |
|
|
|
| Next Vertex (R) |
-0.625 |
8.90625 |
-1048 |
R |
Compute
Cw |
| Cw
= |
7.34375 |
4.101563 |
129 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 11
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
11.875 |
10.78125 |
194 |
B |
|
| Next
Best (N) |
7.34375 |
4.101563 |
129 |
N |
|
| Sum |
19.21875 |
14.88281 |
|
|
|
| P bar |
9.609375 |
7.441407 |
|
|
|
| Worst (W) |
-2.5 |
0.625 |
-217 |
W |
|
| P bar - W |
12.10938 |
6.816407 |
|
|
|
| Next Vertex (R) |
21.71875 |
14.25781 |
-1016 |
R |
Compute
Cw |
| Cw
= |
3.554688 |
4.033203 |
208 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 12
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
3.554688 |
4.033203 |
208 |
B |
|
| Next
Best (N) |
11.875 |
10.78125 |
194 |
N |
|
| Sum |
15.42969 |
14.81445 |
|
|
|
| P bar |
7.714844 |
7.407227 |
|
|
|
| Worst (W) |
7.34375 |
4.101563 |
129 |
W |
|
| P bar - W |
0.371094 |
3.305664 |
|
|
|
| Next Vertex (R) |
8.085938 |
10.71289 |
162 |
R |
Compute
Cr |
| Cr
= |
7.900391 |
9.060058 |
255 |
|
Use
Cr |
|
|
|
|
|
|
|
Step 13
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
7.900391 |
9.060058 |
255 |
B |
|
| Next
Best (N) |
3.554688 |
4.033203 |
208 |
N |
|
| Sum |
11.45508 |
13.09326 |
|
|
|
| P bar |
5.727539 |
6.546631 |
|
|
|
| Worst (W) |
11.875 |
10.78125 |
194 |
W |
|
| P bar - W |
-6.14746 |
-4.23462 |
|
|
|
| Next Vertex (R) |
-0.41992 |
2.312012 |
-43 |
R |
Compute
Cw |
| Cw
= |
8.80127 |
8.66394 |
274 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 14
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
8.80127 |
8.66394 |
274 |
B |
|
| Next
Best (N) |
7.900391 |
9.060058 |
255 |
N |
|
| Sum |
16.70166 |
17.724 |
|
|
|
| P bar |
8.35083 |
8.861999 |
|
|
|
| Worst (W) |
3.554688 |
4.033203 |
208 |
W |
|
| P bar - W |
4.796143 |
4.828796 |
|
|
|
| Next Vertex (R) |
13.14697 |
13.6908 |
101 |
R |
Compute
Cw |
| Cw
= |
5.952759 |
6.447601 |
268 |
|
Use
Cw |
|
|
|
|
|
|
|
Step 15
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
8.80127 |
8.66394 |
274 |
B |
|
| Next
Best (N) |
5.952759 |
6.447601 |
268 |
N |
|
| Sum |
14.75403 |
15.11154 |
|
|
|
| P bar |
7.377014 |
7.555771 |
|
|
|
| Worst (W) |
7.900391 |
9.060058 |
255 |
W |
|
| P bar - W |
-0.52338 |
-1.50429 |
|
|
|
| Next Vertex (R) |
6.853638 |
6.051483 |
269 |
R |
Use
R |
| R
= |
6.853638 |
6.051483 |
269 |
|
Use
R |
|
|
|
|
|
|
|
Step 16
|
|
|
|
|
|
| Coordinates |
A |
B |
Response |
Rank |
|
| Best
(B) |
8.80127 |
8.66394 |
274 |
B |
|
| Next
Best (N) |
6.853638 |
6.051483 |
269 |
N |
|
| Sum |
15.65491 |
14.71542 |
|
|
|
| P bar |
7.827454 |
7.357712 |
|
|
|
| Worst (W) |
5.952759 |
6.447601 |
268 |
W |
|
| P bar - W |
1.874695 |
0.910111 |
|
|
|
| Next Vertex (R) |
9.702148 |
8.267822 |
246 |
R |
Compute
Cw |
| Cw
= |
6.890106 |
6.902657 |
279 |
|
Use
Cw |
After 16 step the best response is 279. The optimum value is 281 when A =
7.54 and 7.46.
|

