|
Home
Optimization Inspection Schedules
Predictive Maintenance Schedules
Engineered Software
Home Page
|
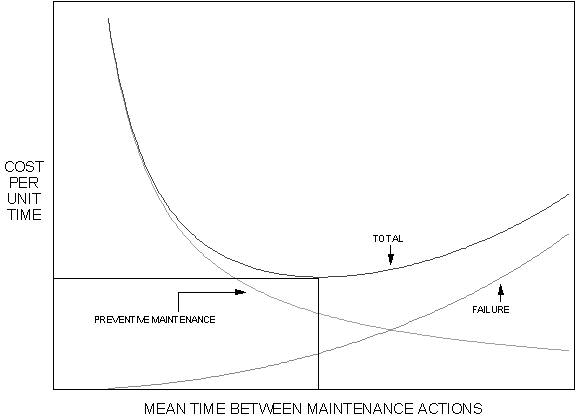
A basic question for a production or maintenance manager is how often to
perform preventive maintenance, or how often to replace components. The
time to fail for an item or system is variable and can be represented by
some probability density function f(t). Referring to the
figure below, the cost of failures per unit time decreases as preventive
maintenance is done more often, but the cost of preventive maintenance per
unit time increases. There exists a point where the total cost of failures
and preventive maintenance per unit time is at a minimum; the optimum
schedule for preventive maintenance.
The assumptions for this routine are:
-
Preventive maintenance is performed on an item at
time = T where T is the optimum schedule between
preventive maintenance.
-
Each time maintenance is performed it is returned
to its initial state, that is, the item is "as good as new."
-
The time to fail follows a Weibull distribution.
The optimum time between maintenance actions is found by minimizing the
total cost per unit time.
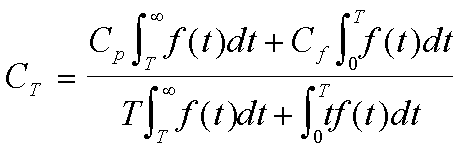
where Cp is the cost of preventive maintenance,
Cf is the cost of a failure, and
T is the time between preventive maintenance actions.
Minimizing the equation above is tedious, and numerical routines are
usually required. Dodson (1994), developed a tabular solution for this
problem given the following assumptions.
- The time to fail follows a Weibull distribution.
- Preventive maintenance is performed on an item at time T at a
cost of Cp.
- If the item fails before time = T, a failure cost of Cf
is incurred.
- Each time preventive maintenance in performed, the item is returned
to its initial state; that is, the item is "as good as new."
The optimum time between preventive maintenance actions is
T = mq + d
where m is a function of the ratio of the failure cost to the
preventive maintenance cost and the value of the shape parameter, and is
given in the table below.
q is the scale parameter of the Weibull
distribution, and
d is the location parameter of the Weibull
distribution.
|
|
ß |
|
Cf/Cp |
1.5 |
2.0 |
2.5 |
3.0 |
4.0 |
5.0 |
7.0 |
10.0 |
|
2.0 |
2.229 |
1.091 |
0.883 |
0.810 |
0.766 |
0.761 |
0.775 |
0.803 |
|
2.2 |
1.830 |
0.981 |
0.816 |
0.760 |
0.731 |
0.733 |
0.755 |
0.788 |
|
2.4 |
1.579 |
0.899 |
0.764 |
0.720 |
0.702 |
0.711 |
0.738 |
0.777 |
|
2.6 |
1.401 |
0.834 |
0.722 |
0.688 |
0.679 |
0.692 |
0.725 |
0.766 |
|
2.8 |
1.265 |
0.782 |
0.687 |
0.660 |
0.659 |
0.675 |
0.713 |
0.758 |
|
3.0 |
1.158 |
0.738 |
0.657 |
0.637 |
0.642 |
0.661 |
0.702 |
0.749 |
|
3.3 |
1.033 |
0.684 |
0.620 |
0.607 |
0.619 |
0.642 |
0.687 |
0.739 |
|
3.6 |
0.937 |
0.641 |
0.589 |
0.582 |
0.600 |
0.627 |
0.676 |
0.730 |
|
4.0 |
0.839 |
0.594 |
0.555 |
0.554 |
0.579 |
0.609 |
0.662 |
0.719 |
|
4.5 |
0.746 |
0.547 |
0.521 |
0.526 |
0.557 |
0.591 |
0.648 |
0.708 |
|
5 |
0.676 |
0.511 |
0.493 |
0.503 |
0.538 |
0.575 |
0.635 |
0.699 |
|
6 |
0.574 |
0.455 |
0.450 |
0.466 |
0.509 |
0.550 |
0.615 |
0.683 |
|
7 |
0.503 |
0.414 |
0.418 |
0.438 |
0.486 |
0.530 |
0.600 |
0.671 |
|
8 |
0.451 |
0.382 |
0.392 |
0.416 |
0.468 |
0.514 |
0.587 |
0.661 |
|
9 |
0.411 |
0.358 |
0.372 |
0.398 |
0.452 |
0.500 |
0.575 |
0.652 |
|
10 |
0.378 |
0.337 |
0.355 |
0.382 |
0.439 |
0.488 |
0.566 |
0.645 |
|
12 |
0.329 |
0.304 |
0.327 |
0.357 |
0.417 |
0.469 |
0.550 |
0.632 |
|
14 |
0.293 |
0.279 |
0.306 |
0.338 |
0.400 |
0.454 |
0.537 |
0.621 |
|
16 |
0.266 |
0.260 |
0.288 |
0.323 |
0.386 |
0.441 |
0.526 |
0.613 |
|
18 |
0.244 |
0.244 |
0.274 |
0.309 |
0.374 |
0.430 |
0.517 |
0.605 |
|
20 |
0.226 |
0.230 |
0.263 |
0.298 |
0.364 |
0.421 |
0.508 |
0.598 |
|
25 |
0.193 |
0.205 |
0.239 |
0.275 |
0.343 |
0.402 |
0.492 |
0.584 |
|
30 |
0.170 |
0.186 |
0.222 |
0.258 |
0.328 |
0.387 |
0.478 |
0.573 |
|
35 |
0.152 |
0.172 |
0.207 |
0.245 |
0.315 |
0.374 |
0.468 |
0.564 |
|
40 |
0.139 |
0.160 |
0.197 |
0.234 |
0.304 |
0.364 |
0.459 |
0.557 |
|
45 |
0.128 |
0.151 |
0.187 |
0.225 |
0.295 |
0.356 |
0.451 |
0.550 |
|
50 |
0.119 |
0.143 |
0.179 |
0.217 |
0.288 |
0.348 |
0.444 |
0.544 |
|
60 |
0.105 |
0.130 |
0.167 |
0.204 |
0.274 |
0.335 |
0.432 |
0.534 |
|
70 |
0.095 |
0.120 |
0.157 |
0.193 |
0.264 |
0.325 |
0.422 |
0.526 |
|
80 |
0.087 |
0.112 |
0.148 |
0.185 |
0.255 |
0.316 |
0.415 |
0.518 |
|
90 |
0.080 |
0.106 |
0.141 |
0.177 |
0.248 |
0.309 |
0.407 |
0.513 |
|
100 |
0.074 |
0.101 |
0.135 |
0.172 |
0.241 |
0.303 |
0.402 |
0.507 |
|
150 |
0.057 |
0.082 |
0.115 |
0.150 |
0.217 |
0.278 |
0.379 |
0.487 |
|
200 |
0.047 |
0.071 |
0.103 |
0.136 |
0.203 |
0.263 |
0.363 |
0.472 |
|
300 |
0.035 |
0.058 |
0.087 |
0.119 |
0.182 |
0.243 |
0.343 |
0.454 |
|
500 |
0.025 |
0.045 |
0.071 |
0.100 |
0.161 |
0.219 |
0.319 |
0.431 |
|
1000 |
0.016 |
0.032 |
0.054 |
0.079 |
0.135 |
0.190 |
0.288 |
0.403 |
Example
The cost of failure for an item is $1000. The cost of preventive
maintenance for this item is $25. The following Weibull distribution
parameters were determined from time to fail data: b
=2.5, q = 181 days, d
= 0. How often should preventive maintenance be done?
Solution
The ratio of failure cost to PM cost is
Cf/Cp = 1000/25 = 40
Entering the table above with this ratio and a shape parameter of 2.5,
gives 0.197 for the value of m.
A PM should be done every
T = (0.197)(181) + 0 = 35.7 days.
|

